WCOJ - WCOJ meets DBSP

Putting together almost everything from the series to create an efficient (complexity-wise) WCOJ algorithm for DBSP.

Some parts of this post have not been heavily scrutinised (by other people), so the content needs to be taken with a grain of salt. It wouldn’t surprise me if something is not quite correct or could be simplified further. I will also abuse some notation a bit. I couldn’t find any reference of combining DBSP with WCOJ in the literature. The only reference that seems relevant is a paper of how to do incremental view maintenance (IVM - the general problem DBSP addresses) for the WCOJ algorithm Leapfrog-Triejoin ¹ and how to do WCOJs in the more powerful incremental computation framework differential dataflow².

Before we start, let’s take a step back and think about what WCOJ for DBSP means. WCOJ in the non-incremental case assures us that we are not doing more work than the largest possible output size of a query ($O(N^{3/2})$ for the triangle query). Combining WCOJ with DBSP means that we are not doing more work than the largest possible output change for a fixed incremental query $Q$ and some changes $\Delta R_i$. Coming back to our beloved triangle query, adding or removing edges in a transaction, can in the worst case lead to $|\Delta triangle|$ being removed or added. In a WCOJ DBSP algorithm we would do never more work than $O(|\Delta triangle|)$ per DBSP tick.

At a high-level we use the multi-join formula from the previous post at each level of the Generic Join algorithm. Consider the triangle query

{:find [?a ?b ?c]
 :where [[?a :g/to ?b]   ;; relation R
         [?a :g/to ?c]   ;; relation S
         [?b :g/to ?c]]} ;; relation T

Let’s say we have the join variable order (?a ?b ?c). As there are only two relations involved per variable the multi-join formula reduces to the standard join formula

where $A^{-1}$ means the relation at the previous tick (the relation delayed by one timestamp).

First we produce a Z-Set containing the prefixes $(a)$ for the results $a$ values appearing in both $R$ and $S$ . The problem is that $R$, $R^\Delta$, $S$ and $S^\Delta$ are Z-sets defined over complete tuples, not key prefixes of $(a)$. The relation $R$ is indexed over tuples $(a, b)$. At the variable-$a$ level, we can enumerate which $a$ values exist, but there’s no single weight for $a$ , but only for complete $(a, b)$ pairs.

We resolve this by treating intermediate levels as unweighted key sets. When doing the first level (variable $a$) in the join process, we’ll actually use a weight of 1 (the multiplicative identity) and these weights are effectively transparent in the join process. Only when binding the final variable of a relation do we use the actual Z-set weights.

For the triangle query with variable order (?a ?b ?c):

• $R$’s weights apply when binding ?b (its final variable in the AEV ordering)
• $S$’s and $T$’s weights apply when binding ?c

This ensures each relation’s weight contributes exactly once to the final result weight. To see how this weight-separation works in practice, let’s first look at how we represent partial results during the join process.

Result representation as Indexed Z-Set’s

In the relational model result sets are often represented as lists of lists. For example consider the following result set of geo-data that becomes finer grained from left to right. 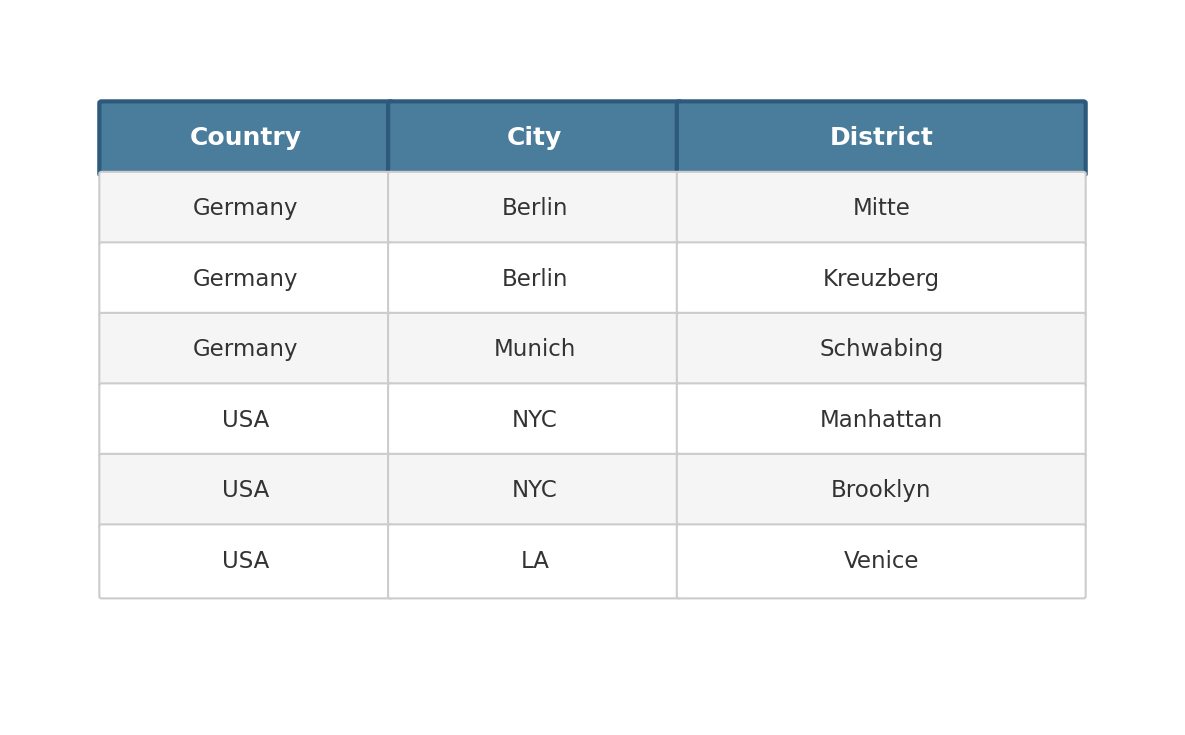In a trie representation (also used in factorized databases) the above would look as follows. 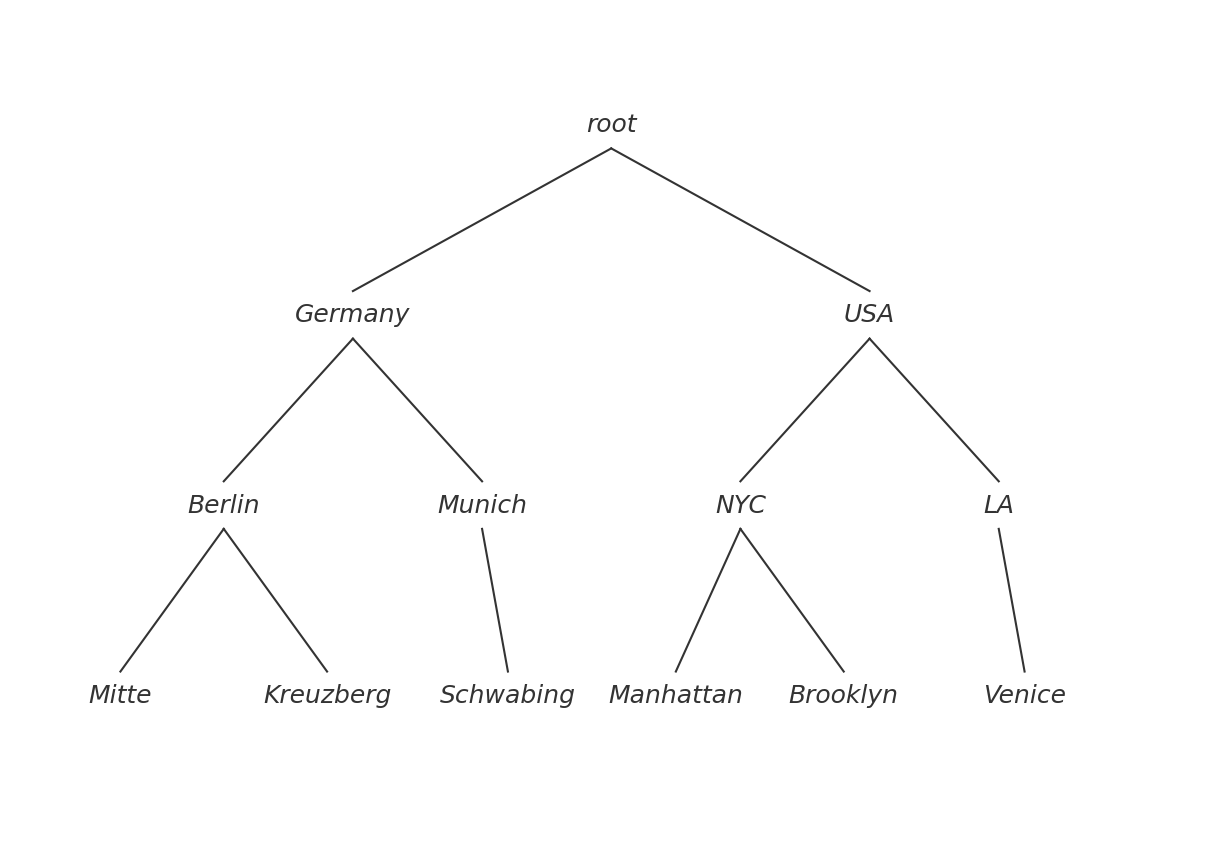If Country, City and District were all join variables in a WCOJ join, this trie structure would be build up as we are joining. Leapfrog-Triejoin³ builds this structure in a DFS manner and GenericJoin⁴ walks this structure in BFS manner (probably good content for another post). When one extends one prefix with extensions in GenericJoin, it essentially means extending a subtree by one level. For example for the prefix (Germany, Berlin) one would create new prefixes (Germany, Berlin, Mitte) and (Germany, Berlin, Kreuzberg). When using persistent lists to represent result tuples in GenericJoin the trie is implicitly encoded by the structural sharing of the persistent lists⁵.

We are going to use indexed Z-sets to represent our results when doing the variable based WCOJ join. Each level of the result trie are the results for one join variable. Paths to leaves represent prefixes. The weight at each leaf is the product of weights from all relations whose variables have been fully bound. Meaning only when the last variable of a relation is being joined the actual weight is being used in the join process (otherwise we use the multiplicative identity 1).

To implement our incremental WCOJ, we need three key operations on indexed Z-sets that let us build up result tries level-by-level while managing weights correctly.

extendLeaves

We add the following helper methods on our IZSet (a generic interface implemented by both Z-sets and indexed Z-sets) implementation.

typealias Prefix = List<Any>

fun extendLeaves(mapFn: (Prefix, W) -> ZSet<K, W>): IndexedZSet<K, W>

extendLeaves works on a Z-set (can be a standard z-set or a (nested) indexed-zset). Given a function that maps from the prefix path of the partial result and the weight to a Z-set, it creates a new indexed Z-set where the prefix has been extended by one level. Using the notation from the previous post and a partial result tree from above with added weights

{"Germany", 
  {"Berlin" 1 
   "Munich" -1} 
 "USA" 
  {"NYC" -1 
   "LA" 1}}

On this example our extendLeaves function would receive

["Germany", "Berlin"] 1
["Germany", "Munich"] -1
["USA", "NYC"] -1
["USA", "LA"] 1

If the mapping function would take the first character of the city key and multiply the weight by two to create a new singleton Z-Set, we would obtain

{"Germany", 
  {"Berlin" {"B" 2} 
   "Munich" {"M" -2}} 
 "USA" 
  {"NYC" {"N" -2} 
   "LA" {"L" 2}}}

getByPrefix and asZSetView

The getByPrefix function returns Z-set at the given prefix path.

fun getByPrefix(prefix: Prefix): IZSet<K, W, *>

For the full hierarchical geo-data example from above:

{"Germany",
  {"Berlin" 
    {"Mitte" -1
     "Kreuzberg" 1} 
   "Munich" 
    {"Schwabing" 1}} 
 "USA" ...}

for the prefix ("Germany", "Berlin"), one would obtain

{"Mitte" -1
 "Kreuzberg" 1} 

The asZSetView function returns the unweighted key set described above when called on an indexed Z-set and just the Z-set itself when called on a standard Z-set.

fun asZSetView(): ZSet<K, W>

For the full geo-data example Z-set we would get

{"Germany" 1
 "USA" 1}

at the top-level and if we chain getByPrefix and zSetView

zset.getByPrefix(listOf("Germany")).asZSetView()

we’d get

{"Berlin" 1
 "Munich" 1}

In our DBSP WCOJ algorithm, indexed Z-sets are fundamentally a structural/organizational layer, they are kind of a trie that partitions the data by a key. At intermediate layers we don’t carry weight information, so the chaining of getByPrefix and asZSetView allows us to obtain Z-Sets with natural weights at intermediate levels and leaf-level weights when the final variable of a relation gets joined.

IncrementalPrefixExtender

The corresponding incremental PrefixExtender interface from WCOJ - Generic Join is given by

interface ZSetPrefixExtender {
    fun count(prefix: Prefix): Int
    fun propose(prefix: Prefix): ZSet<Extension, IntegerWeight>
    fun intersect(prefix: Prefix, extensions: ZSet<Extension, IntegerWeight>): ZSet<Extension, IntegerWeight>
}

In intermediate Z-Set operations of a DBSP pipeline it might happen that the multiplicities become quite large. To guard against the possibility of an overflow we use IntegerWeight , which is a custom implementation of int. A ZSetPrefixExtender at the base level (when we use a base data pattern à la [?a :g/to ?b]) in the algorithm will be backed by an indexed Z-set of one of the permutations of the EAV index. At each timestamp tick both $EAV^\Delta$ and $EAV^{-1}$ (or some other permutation of a base index). From the fixed part of the query and a given prefix we look up the nested (indexed) Z-set. The size of this Z-set is the count of potential extensions. propose returns the Z-Set view of the index via chained getByPrefix and zSetView calls. intersect does an equi-join with this Z-set view and the passed in Z-set.

IncrementalIndex

In the DBSP framework the operators work on streams (a sequence of Z-sets) and this is definitely the better abstraction if you want to implement rules and recursive queries. As I mainly wanted to get something correct working for standard EDN Datalog data patterns, I opted for a simpler eval/commit approach. eval receives the Z-sets from upstream operators or the changed base level relations and commit updates the state of the operators with the recent changes. This works well for tree-like pipelines (no recursive queries) as the time dimension is strictly ordered. One eval + commit call per tick.

interface IncrementalIndex : LevelParticipation {
    /** Receive the delta for this transaction */
    fun receiveDelta(delta: ZSetIndices)

    /** Merge current delta into accumulated state (call after join completes) */
    fun commit()

    /** Extender over the current delta */
    val delta: ZSetPrefixExtender

    /** Extender over z⁻¹ (accumulated previous state) */
    val accumulated: ZSetPrefixExtender
}

An IncrementalIndex receives the updates (ZSetIndices) to the base indices via receiveDelta. For composite Datalog Connectors the IncrementalIndex passes the updates to it’s children. It further exposes the delta and the accumulated state of the current iteration as ZSetPrefixExtender. After the changes have been processed the accumulated state gets updated via the commit method.

With all of this machinery in place we can finally turn to a WCOJ DBSP algorithm.

IncrementalGenericJoin

The code for the IncrementalGenericJoin is now pretty straightforward (at least to me 😅).

class IncrementalGenericJoin(private val relations: List<IncrementalIndex>, private val levels: Int) : IncrementalJoin<ResultTuple> {
    /**
     * Compute delta extensions for one level using the DBSP incremental formula:
     *
     * Δ_{1..n} builds up as: Δ_{1..i} = Δ_{1..i-1} ⋈ Δᵢ
     *                                 + Δ_{1..i-1} ⋈ z⁻¹(i)
     *                                 + Δᵢ ⋈ z⁻¹(processed relations)
     */
    private fun computeLevelDelta(prefix: Prefix, relations: List<IncrementalIndex>): ZSet<Extension, IntegerWeight> {
        if (relations.isEmpty()) return ZSet.empty()

        // Start with smallest delta (WCOJ optimization)
        val minIndex = relations.indices.minBy { relations[it].delta.count(prefix) }
        var runningDelta = relations[minIndex].delta.propose(prefix)

        for (j in relations.indices) {
            if (j == minIndex) continue

            val deltaJ = relations[j].delta.propose(prefix)
            var term3 = deltaJ

            // Intersect with z⁻¹ of all relations processed before j
            for (k in 0 until j) {
                term3 = relations[k].accumulated.intersect(prefix, term3)
            }

            // Don't forget minIndex if it comes after j
            if (minIndex > j) {
                term3 = relations[minIndex].accumulated.intersect(prefix, term3)
            }

                           // Δ_{1..i-1} ⋈ Δᵢ
            runningDelta = runningDelta.equiJoin(deltaJ) +
                           // + Δ_{1..i-1} ⋈ z⁻¹(i)
                           relations[j].accumulated.intersect(prefix, runningDelta) +
                           // + Δᵢ ⋈ z⁻¹(1) ⋈ z⁻¹(2) ⋈ ... ⋈ z⁻¹(i-1)
                           term3
        }

        return runningDelta
    }

    override fun join(deltas: ZSetIndices): ZSet<ResultTuple, IntegerWeight> {
        // 1. Distribute deltas
        relations.forEach { rel -> rel.receiveDelta(deltas) }

        // 2. Compute join level by level
        val participatingLevel1 = relations.filter { it.participatesInLevel(0) }
        var result: IZSet<Any, IntegerWeight, *> = computeLevelDelta(emptyList(), participatingLevel1)

        for (level in 1 until levels) {
            val participating = relations.filter { it.participatesInLevel(level) }
            result = result.extendLeaves { prefix, weight ->
                computeLevelDelta(prefix, participating).multiply(weight)
            }
        }

        // 3. Commit deltas
        relations.forEach { it.commit() }

        return result
    }
}

The join receives the deltas and first distributes them across the IncrementalIndex relations. Afterwards the algorithm uses the multi-join formula from the previous post to extend (via extendLeaves) a partial result trie level by level via computeLevelDelta . computeLevelDelta is just the multi-join formula enshrined in code, but it also receives the prefix of the current sub-tree being extended so that the ZSetPrefixExtenders can constrain their respective Z-sets. After the Z-Set of the new level is computed it gets scalar multiplied by the weight of the sub-tree currently being extended. Until the result set (result trie) has been fully built up, the weight of the partial result trie leafs is the contribution of all relations where all variables have been fully exhausted in the WCOJ process. If one takes the triangle query again

When only variables $A$ and $B$ have been joined so far, the result trie leaf weights will only contain the weight contribution from $R$ even if the $(a, b)$ prefixes have also been validated against $S$ and $T$ respectively. Their weight contribution applies when $C$ gets joined.

Please note that all of the implementations above are purely educational, meaning that all of this will likely have bad constants in practice. This is WCO in terms of big $O$ complexity, but might fare badly in practice and you may be better off doing good old binary joins.

I think it would be good to fully formalize this WCOJ algorithm (or some simplification thereof) as a DBSP circuit.

The central premise of this post is that doing WCOJ in DBSP is worth it. Datomic style engines are mostly entity-centric and for most use cases don’t have cyclic queries (where WCOJ shines). If you’d want graph data pattern matching you likely reach for a graph database (the algorithm described here still applies, but the indices might be quite different).
The incoming deltas are likely quite small, so is the cost (likely high constants) incurred by all the complex maintenance and joins of Z-sets worth it, or would a left-deep join tree with good statistics fare almost always better? Something to figure out.

This was the post I wanted to get at when starting the WCOJ series. There is more to write about, so I guess there will be more posts, but it might be a while until I get to them.